
Wie sich die Normalisierung auf dunkle Helligkeiten auswirkt
Der zweite Schritt, der die RGB-Werte auf unsere nicht-lineare Empfindung der Helligkeit skaliert, verläuft in ähnlicher Weise wie die Transformation zwischen Y im XYZ und dem L* im L*a*b* und wird ... Tata ... Gammakorrektur genannt. Viele RGB-Farbräume benutzen eine einzige Zahl, um das Gamma wiederzugeben: z.B. 1.8 für AppleRGB und 2.2 für AdobeRGB.
Farbräumen wie sRGB und NTSC wurden allerdings mit einem komplexeren mathematischen Ausdruck für Gamma definiert. Der Gebrauch einer einzigen Zahl für das Gamma erzeugt in den meisten Anwendungen unrelevante Fehler, kann aber in kritischen Anwendungen (in der Bildverarbeitung, aber auch bei Farbkorrekturen in der Bildbearbeitung) bei Transformationen zu signifikanten Fehlern in Farben mit geringer Helligkeit (in dunklen Farben also) führen.
Wenn wir eine Farbe in der RGB-Notation in einer Anwendung wählen, wählen wir tatsächlich R’G’B’-Werte – also ein Gamma-korrigiertes RGB.

Zum Verständnis: Das Diagramm zeigt eine „Rückwärtstransformation“. Wir sehen auf dem Display des Computers tatsächlich R’G’B’, das wir aber als RGB bezeichnen!
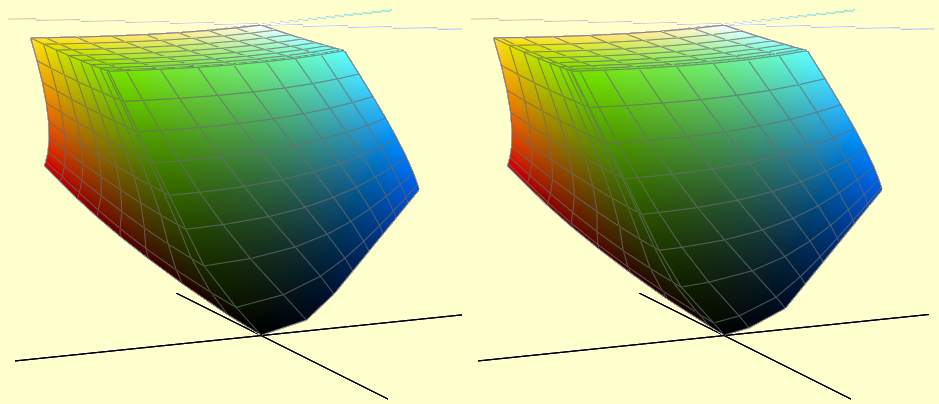
Der gelbe Würfel auf der linken Seite zeigt einen R’G’B’-Farbraum, der in fünf gleich große Zonen für jede Koordinate unterteilt ist. Der blaue und der rote Würfel auf der rechten Seite zeigen, wie der blaue Würfel in ein lineares RGB transformiert wird. Der blaue Würfel zeigt das Verhalten bei einem Gamma von 1.8, wie es für ColorMatch oder AppleRGB verwendet wird und der rote Würfel zeigt die Auswirkungen der Transformation für ein Gamma von 2,2, wie es bei AdobeRGB verwendet wird (und das eine gute Näherung des komplexen Gammas des sRGBs darstellt). Wir sehen, dass viele R’G’B’-Kombinationen in den relativ kleinen Würfeln nahe bei RGB=(0,0,0) liegen, während die größte Zone nahe bei RGB=(255,255,255) liegt. Man könnte auch sagen, dass den dunklen Bereichen mehr R’G’B’-Koordinaten zugeordnet sind.
Gamma-korrigierte RGB-Werte werden eigentlich mit R’G’B’ bezeichnet, um sie von den linearen RGB-Daten zu unterscheiden. Der kleine Plot, dass wir dennoch überall „RGB“ lesen, verbirgt ein paar Erkenntnisse über RGB-Farbräume und Transformationen. In einem R’G’B’-Farbraum stecken mehr Koordinaten für die niedrigen (dunklen) Helligkeiten als für die hohen Helligkeiten. Und zu allem Überfluss stecken in einem R’G’B bei einem höheren Gamma noch mehr Koordinaten in den dunklen Helligkeiten als bei einem geringeren Gamma.
Nachdem wir einen Schritt zurück von R’G’B’ nach RGB gemacht haben, warum sollten wir nicht noch einen Schritt weiter zurück von RGB nach xyY machen? Da wir mit XYZ-Daten arbeiten wollen, brauchen wir eine Farbtemperatur und die Primärfarben.
Im xyY-Diagramm sehen wir, dass viele Farben an der Peripherie des RGB-Farbraums gepackt liegen (komprimiert).